学习神经网络背后的数学模型[译]
Chen Hao posted on 23 Aug 2018如今我们如果需要创建一个神经网络,可以很方便地使用Keras,TensorFlow或PyTorch等专业的库和框架来实现。即使是一个结构非常复杂的神经网络,也只需要几行代码。我们不需要过多担心权重矩阵的大小,也不需要记住我们使用的activation function的导数公式。这使得我们花在程序debug的时间大大减少,并简化了我们的工作。然而,了解神经网络内部的数学模型对于我们诸如架构选择,超参数调整或优化等都有很大的帮助。为了更多地了解神经网络是如何工作的,我决定花一些时间来研究下在这些框架下面隐藏的数学模型,并且总结和分享在这遍文章中。
作为一个例子,我们来解决如图1所示的一个二元分类问题。这个分类问题对于许多传统的Machine Learning算法来说是不太容易的,但是神经网络确可以很轻松地驾驭。
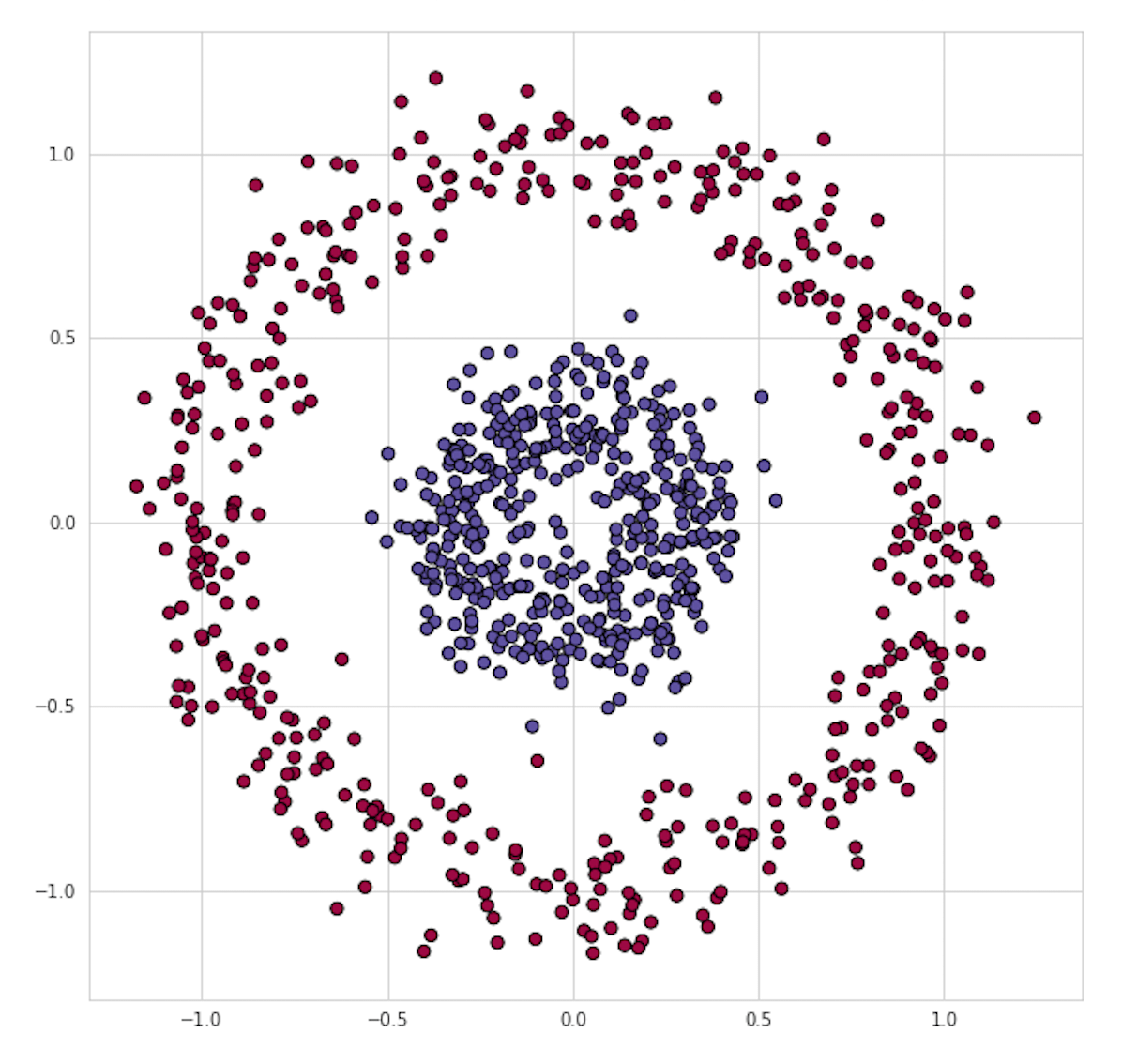
图1.可视化训练数据集
为了解决这个问题,我们将构建一个如图2所示的神经网络模型。其中包括五个完全连接的layers,每一个layer具有不同数量的units。我们将使用ReLU作为hidden layers的activation function,然后使用Sigmoid作为output layer的activation function。 这是一个非常简单的架构,但足以帮助我们阐明神经网络的一些核心理念和数学原理。
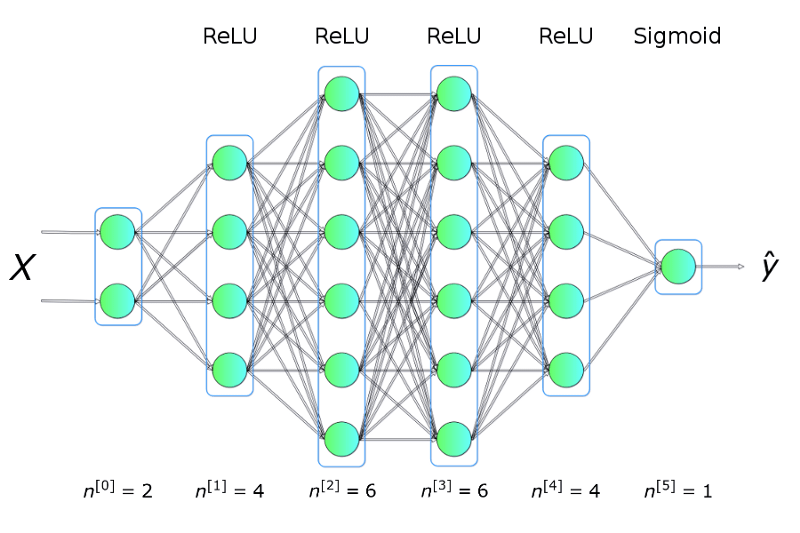
图2.神经网络架构
用Keras快速搭建一个神经网络模型
首先,我使用最受欢迎的机器学习库之一-KERAS来快速实现一下上面我们构建的神经网络模型。
from keras.models import Sequential
from keras.layers import Dense
model = Sequential()
model.add(Dense(4, input_dim=2,activation='relu'))
model.add(Dense(6, activation='relu'))
model.add(Dense(6, activation='relu'))
model.add(Dense(4, activation='relu'))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='binary_crossentropy', optimizer='adam', metrics=['accuracy'])
model.fit(X_train, y_train, epochs=50, verbose=0)
就这样就完成了,并且这个模型能几乎能以100%的准确度对我们的测试数据进行分类。通过下面的动图我们来直观的感受下隐藏在模型背后的训练过程:
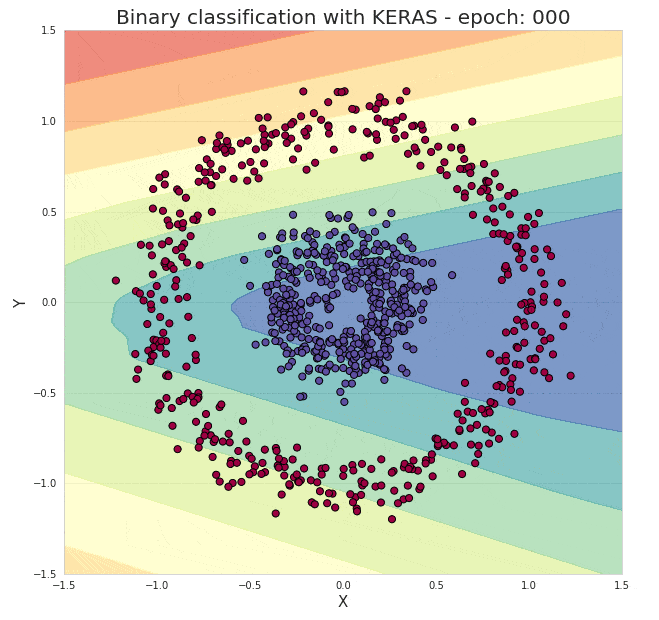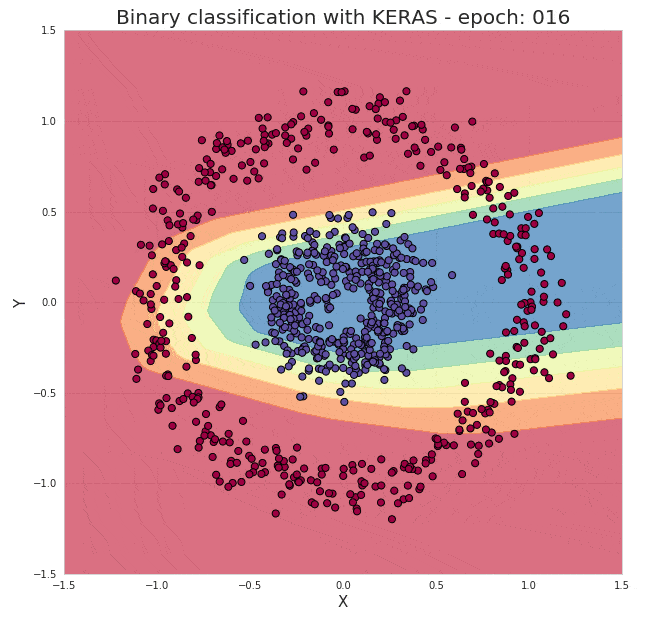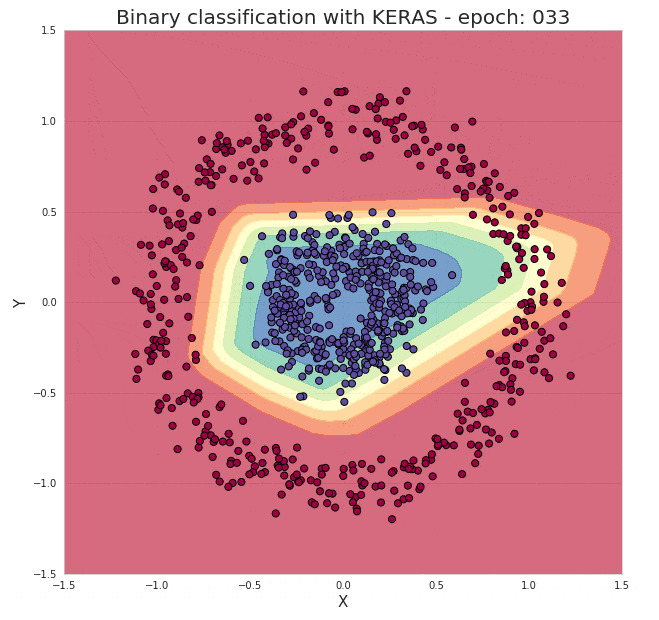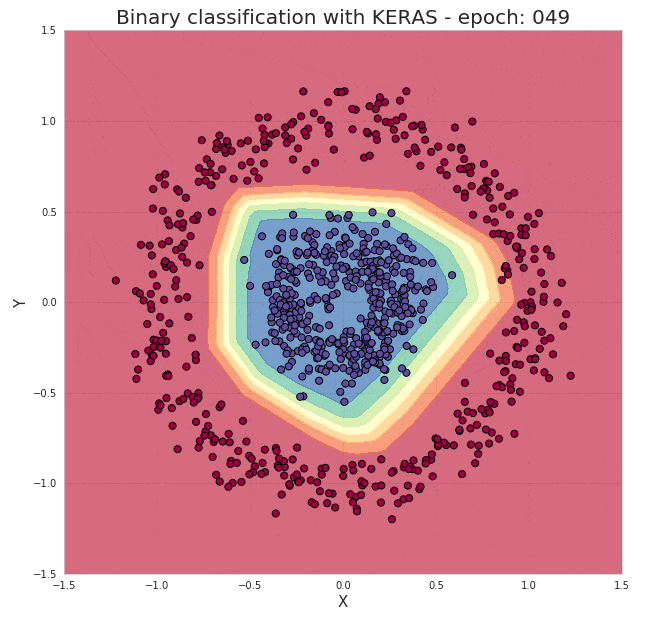
图3. 图示神经网络训练过程
Neural Network
那么到底什么是神经网络(Neural Network)?简单来讲,它是一种受生物学启发来构建计算学习程序的方法,能够独立学习并找到数据中的连接关系。如图2所示,神经网络是按layer排列的多个‘neurons’的集合,以相互通信的方式连接在一起。接下来我们展开来各个突破这其中的概念。
1. Neuron
每个神经元接收一组$x$值(编号从$1$到$n$)作为输入并计算预测的$\hat{y}$值。向量$x$是训练集的$m$个示例中的其中之一。每个单元则都有自己的一组参数,通常称为$w$(权重列向量)和$b$(偏差),它们在学习过程中发生变化。在每次迭代中,神经元基于其当前权重向量$w$和偏差$b$来计算向量$x$的加权平均值。最后,通过一个非线性激活函数$g$来得到最终计算结果。
\[z = w_1x_1 + w_2x_2 + w_3x_3 + \dotsc + w_nx_n = w^T\cdot{x}\]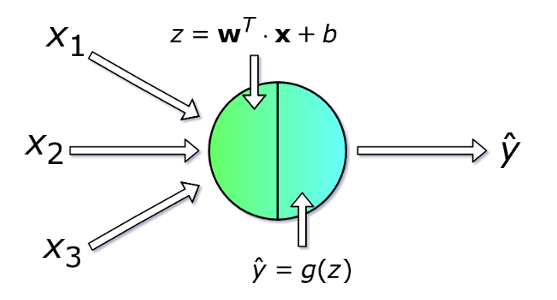
图4.单个neuron
2. Layer
现在我们稍微扩大一下视角,考虑如何对整个神经layer进行计算。 我们将结合上面我们对单个unit内计算的了解,拓展到对在整个layer中计算的矩阵化计算。为了统一符号,我们将所选layer标记为$l$,下标$i$则表示该layer在神经网络中的索引。
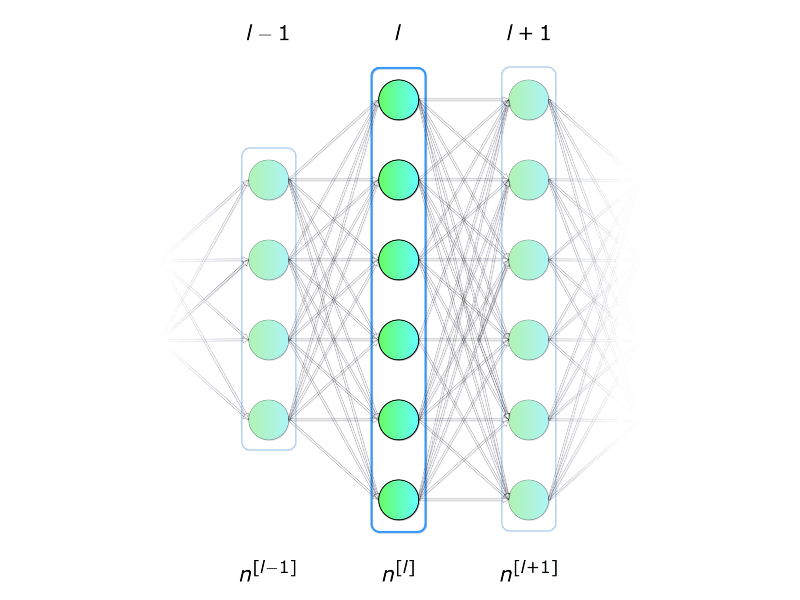
图5.单个layer
还有一个重要的评论:当我们为单个neuron编写方程时,我们使用$x$和$\hat{y}$来分别标记数据集的列向量和预测值。 当切换到layer时,我们使用向量$a$表示相应layer的激活向量。 因此,$x$向量可以看成是layer 0(input layer) 的激活向量。 每个layer中的每个neuron unit其实都执行类似以下公式的计算:
\[z_i^{[l]} = w_i^T \cdot a^{[l-1]} + b_i \hspace{1cm} a_i^{[l]} = g^{[l]}(z_i^{[l]})\]为了清楚起见,让我们写下第二个layer的完整计算公式
\[z_1^{[l]} = w_1^T \cdot a^{[l-1]} + b_1 \hspace{1cm} a_1^{[l]} = g^{[l]}(z_1^{[l]}) \\ z_2^{[l]} = w_2^T \cdot a^{[l-1]} + b_2 \hspace{1cm} a_2^{[l]} = g^{[l]}(z_2^{[l]}) \\ z_3^{[l]} = w_3^T \cdot a^{[l-1]} + b_3 \hspace{1cm} a_3^{[l]} = g^{[l]}(z_3^{[l]}) \\ z_4^{[l]} = w_4^T \cdot a^{[l-1]} + b_4 \hspace{1cm} a_4^{[l]} = g^{[l]}(z_4^{[l]}) \\ z_5^{[l]} = w_5^T \cdot a^{[l-1]} + b_5 \hspace{1cm} a_5^{[l]} = g^{[l]}(z_5^{[l]}) \\ z_6^{[l]} = w_6^T \cdot a^{[l-1]} + b_6 \hspace{1cm} a_6^{[l]} = g^{[l]}(z_6^{[l]}) \\\]对于每个layer,我们都执行类似的操作。使用for循环效率不高,因此为了加快计算速度,我们将计算矢量化。首先,通过将权重$w$(转置)的水平向量堆叠在一起,我们将构建矩阵$W$.类似地,我们将在层中的每个neuro的偏差堆叠在一起,从而创建垂直偏差向量$b$。 现在就可以通过矩阵运算来一次对一个layer的所有neuro进行计算。 图解如下:
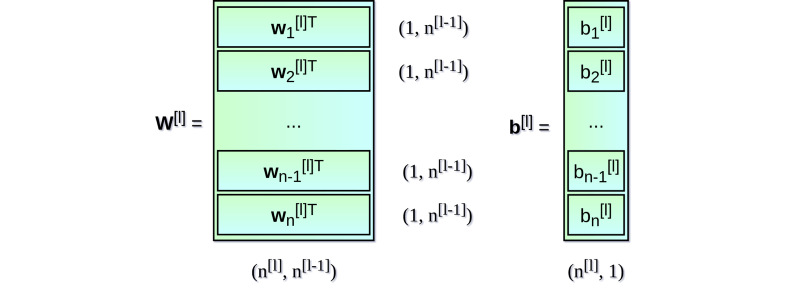
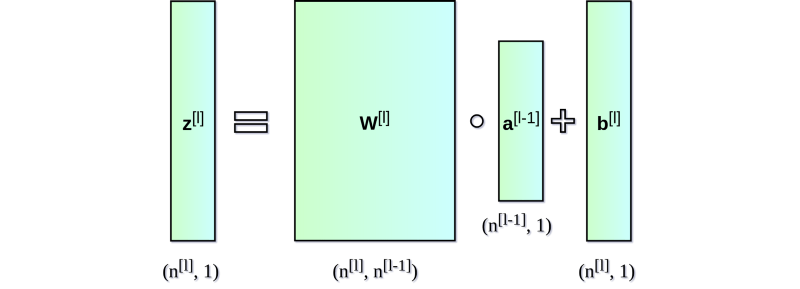
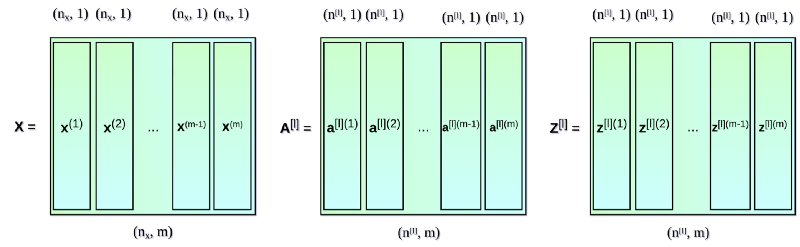
到目前为止我们制定的等式只涉及数据集中的一个条目。 在神经网络的学习过程中,您通常使用大量数据,最多可达数百万条。 因此,下一步对所有条目矢量化运算。 假设我们的数据集中有$m$个条目,每个条目都有$nx$个特征。 首先,我们将每层的垂直向量$x$,$a$和$z$组合在一起,分别创建$X$,$A$和$Z$矩阵。 然后我们用新创建的矩阵重新编写之前的方程式:
3. Activation Function
Activation function(激活函数)是神经网络的关键元素之一。 没有它,我们的神经网络只是多个线性函数的组合。 这样的模型能解决的问题就比较显示,不会比逻辑回归强到哪里。 非线性变化能给学习过程提供更大的灵活性和创建更复杂功能。 Activation function的选择对深度学习的速度有显著的影响,这也是我们选择activation function一个重要参考因素。 图6显示了一些常用的activation function。 目前,在hidden layer最受欢迎的activation function可能是ReLU。 当我们处理二进制分类并且我们希望模型返回的值在0到1的范围内时,我们则通常在output layer选择sigmoid函数。
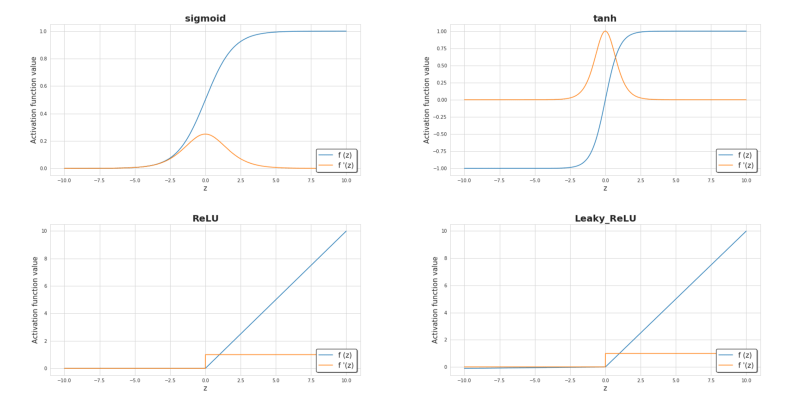
图6.常用activation functions
4. Loss function
Loss function是我们了解学习过程进展的基本信息来源。一般来说,Loss function旨在衡量模型现有的准确度与“理想”解决方案之间的差距。在我们这个例子中,我们使用binary crossentropy作为我们的loss function。实际运用中根据问题的不同,我们选用相应最合适loss function。下面是binary crossentropy的公式描述,以及在学习过程中Loss function的值和模型准确度在每次迭代中的变化关系。
\[J(W,b) = \frac{1}{m} \sum_{i=1}^{m} L(\hat{y}^{(i)}, y^{(i)}) \\ L(\hat{y},y) = - ( ylog\hat{y} + (1-y)log(1-\hat{y}))\]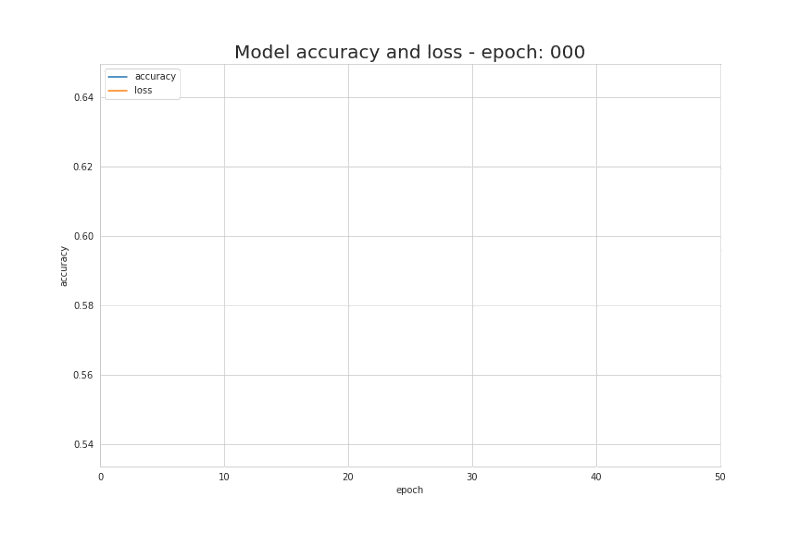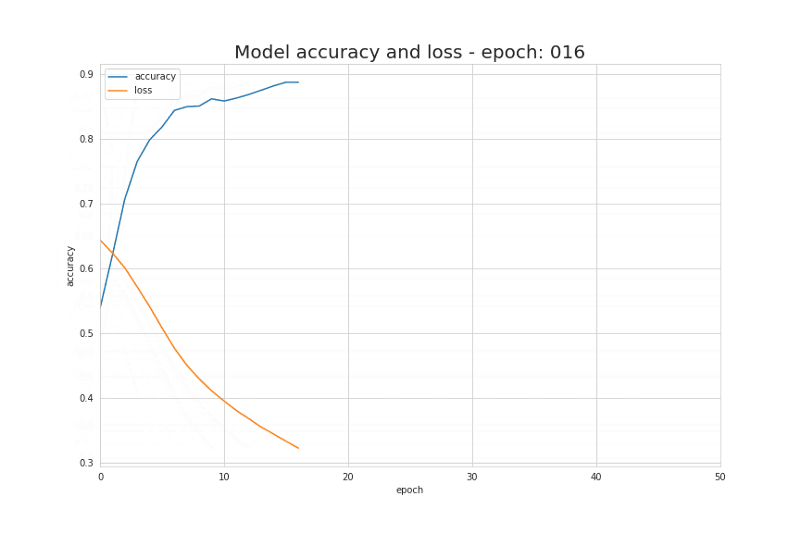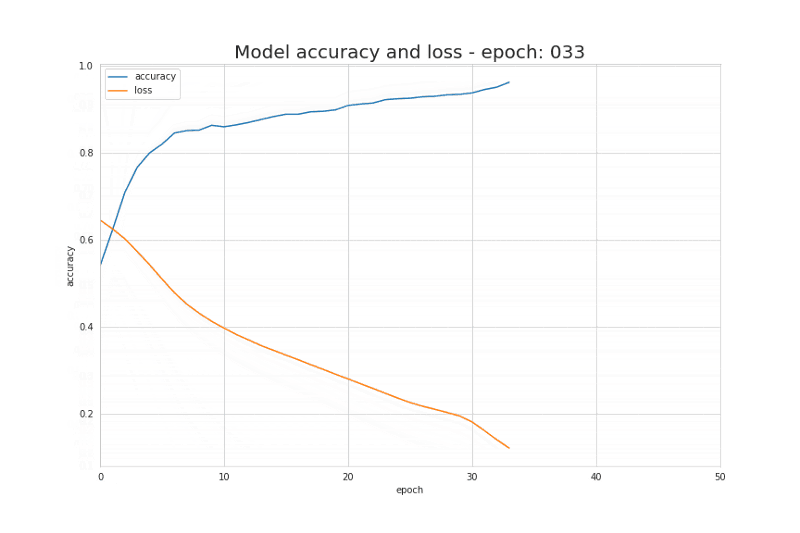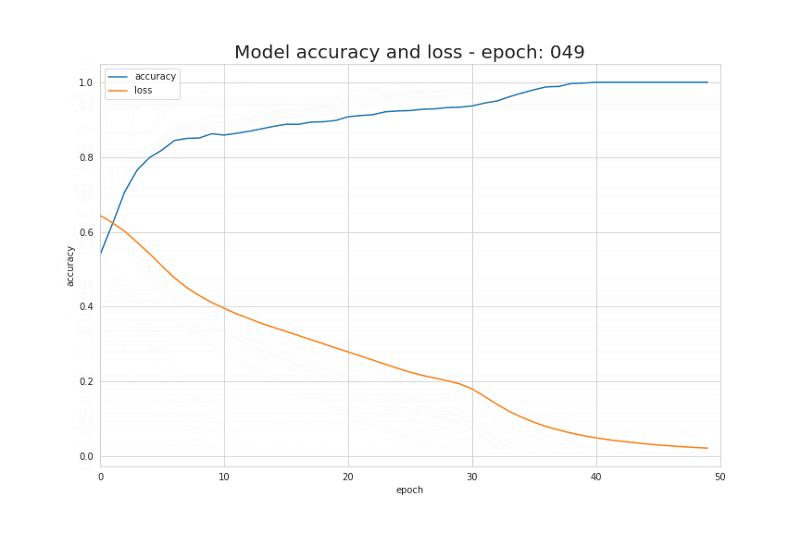
图7.学习过程中loss function的值和模型accurancy的变化曲线
5. Backpropagation
神经网络训练的学习过程就是不断修改$W$和$b$参数,最终使loss function的返回值最小化的过程。为了实现这一目标,就不得不使用到微积分,使用gradient descent方法找到函数最小值。在每次迭代中,我们将相对于我们的神经网络的每个参数计算loss function偏导数的值。对于偏导,这里只是简单提一下,导数具有很好的描述函数在某个点斜率的能力。通过计算偏导数我们就知道参数修正的方向。下面的这个图展示了学习过程中参数优化的实际过程。
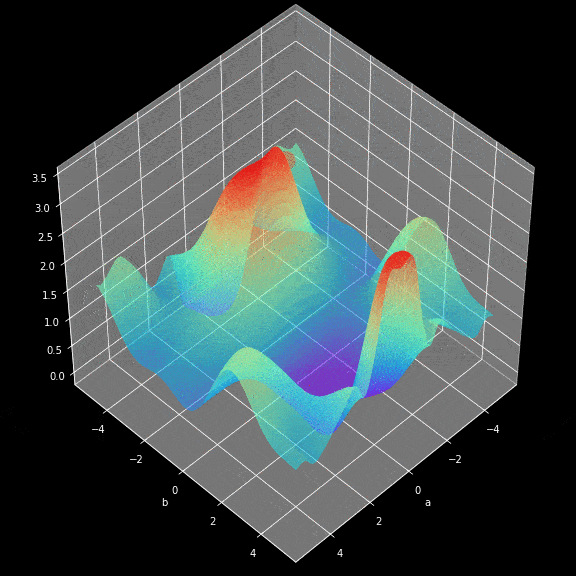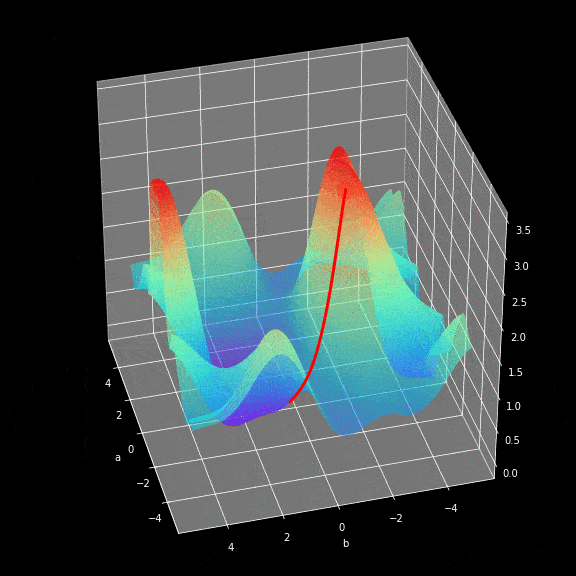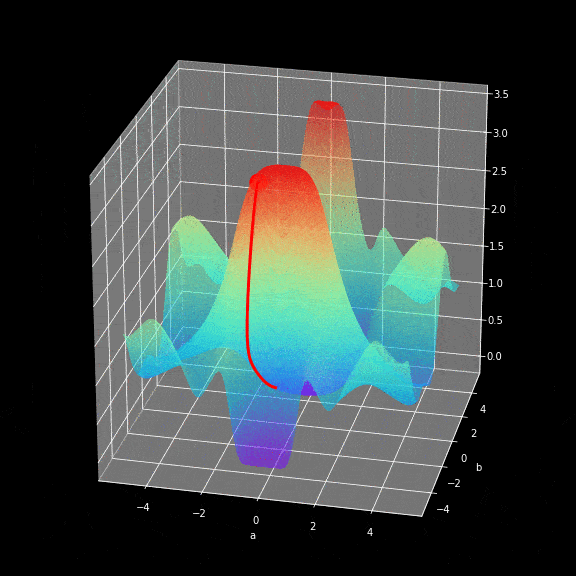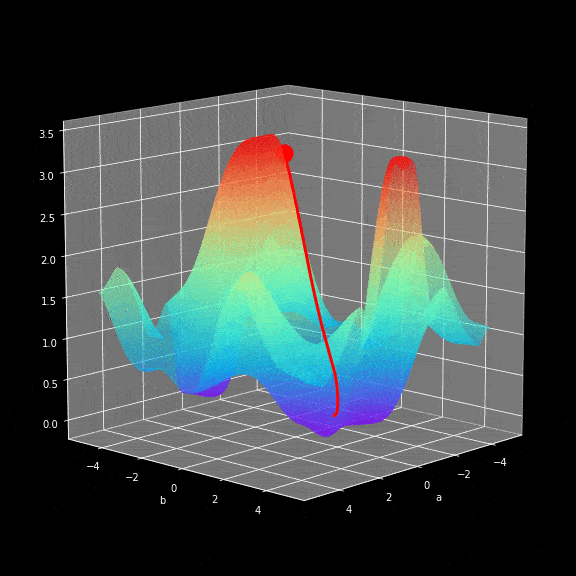
图8.gradient descent图示
在我们的构建的神经网络中,学习过程与上图中类似,但是我们的参数更多,优化起来就比较复杂,这里我们需要介绍另外一种函数优化算法Backpropagation。Backpropagation允许我们计算一个非常复杂的梯度来帮助我们调整神经网络的参数:
\[W^{[l]} = W^{[l]} - \alpha \mathrm d{W^{[l]}} \\ b^{[l]} = b^{[l]} - \alpha \mathrm d {b^{[l]}} \\ \mathrm d{W^{[l]}} = \frac {\partial L} {\partial W^{[l]}} = \frac {1}{m} \mathrm d Z^{[l]} A^{[l-1]T} \\ \mathrm d{b^{[l]}} = \frac {\partial L} {\partial b^{[l]}} = \frac {1}{m} \sum_{i=1}^{m} \mathrm d Z^{[l](i)} \\ \mathrm d{A^{[l-1]}} = \frac {\partial L} {\partial A^{[l-1]}} = W^{[l]T} \mathrm d Z^{[l]} \\ \mathrm d{Z^{[l]}} = \mathrm d{A^{[l]}} * g'(Z^{[l]})\]在上面的等式中,$\alpha$表示learning rate - 一个超参数。learning rate的选择对于神经网络的训练效果至关重要 - 如果我们将其设置得太低,我们的神经网络学习得就非常慢,如果设置得太高我们就很难得到最优参数。图9显示了神经网络中的操作顺序,这里我们可以清楚地看到Forward and Backward Propagation如何协同工作来优化loss function:
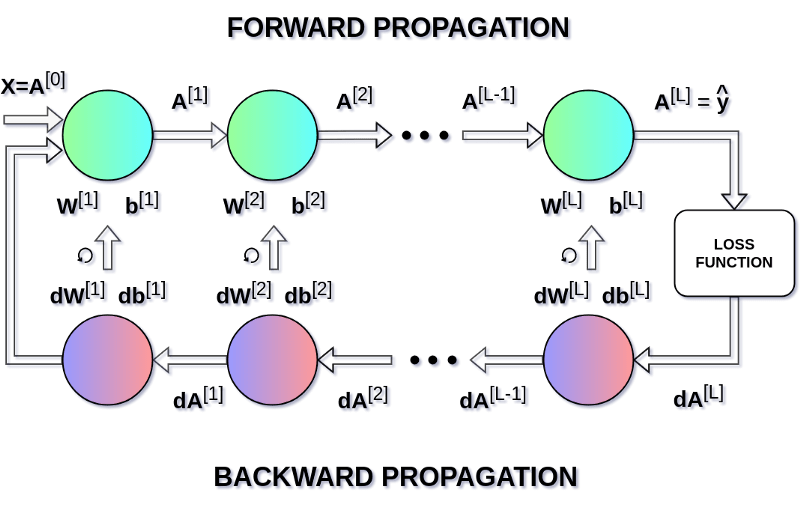
图9.Forward and Backward Propagation
小结
希望大致讲清楚了神经网络的主要数学模型,这里分享的只我个人认为最重要的几个点,但也只是冰山一角。如果有兴趣,强烈建议动手写一个小型神经网络,不使用高级框架,只能使用Numpy,试一下。