Two Sample Binomial Tests

This is my course notes for Mathematical Biostatistics Boot Camp 2, course materials are free on github.

Tests for contingency table data

1.The Score Test

1.1 The score test statistics

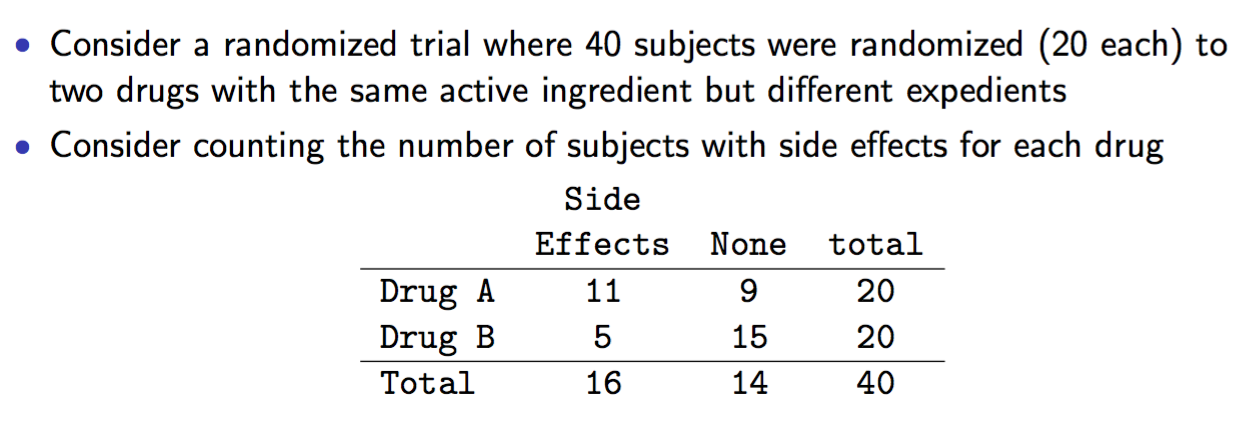
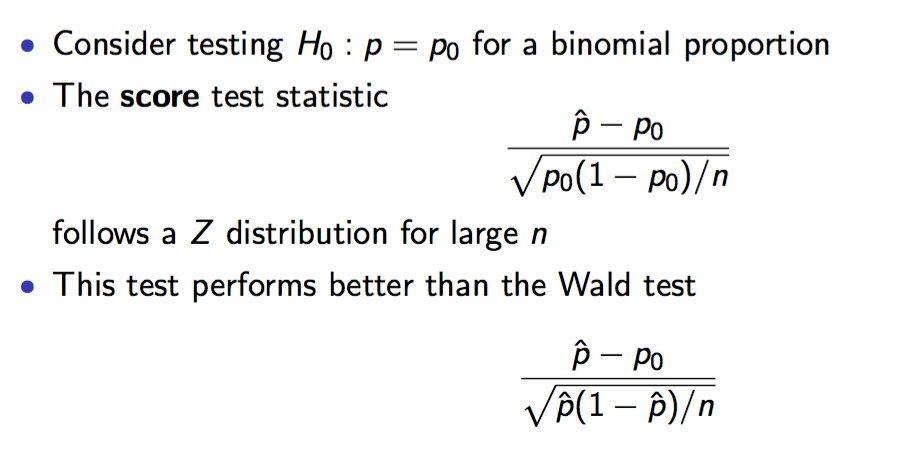
1.2 Calculate confidence interval

In the one sample case, the Wald interval and test performs poorly relative to the score interval and test. For testing, always use the score test.For intervals, inverting the score test is hard and not offered in standard software. the Agresti/Caffo interval does not approximate the score interval, but does perform better than the Wald interval.

1.3 Exact binomial tests

2. Comparing two binomials

2.1 Absolute change

2.2 Relative change

2.3 Odds ratio

2.4 Summary and Comments

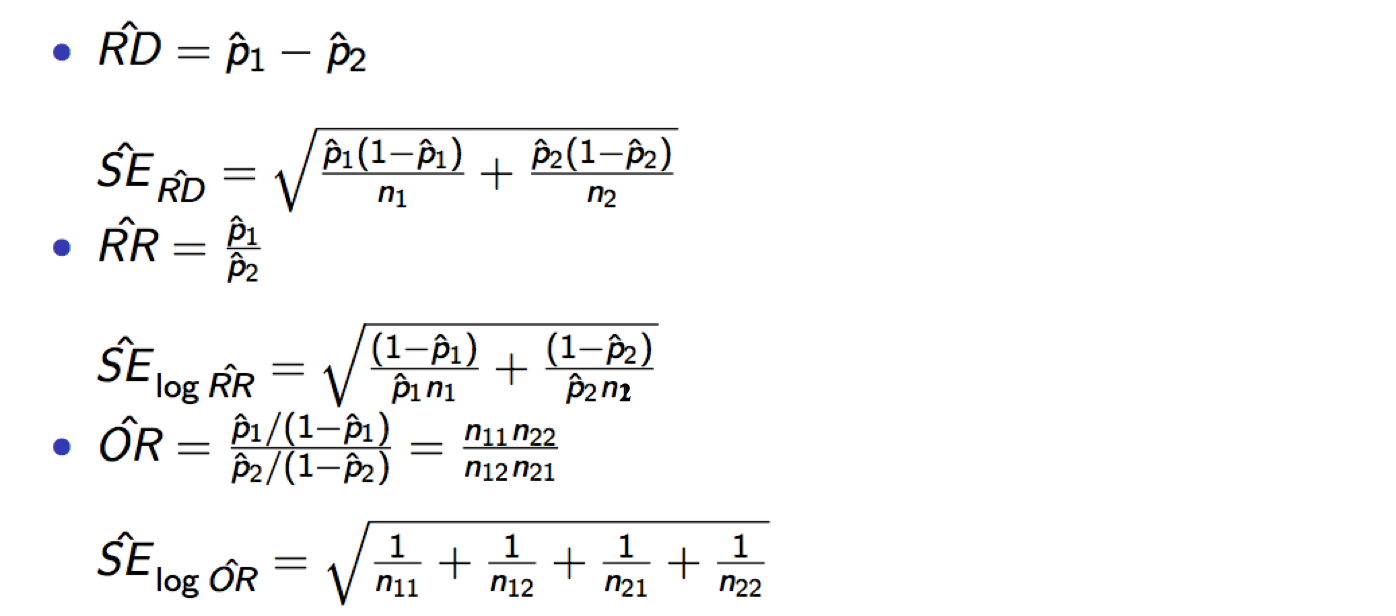
3. Fisher’s exact test

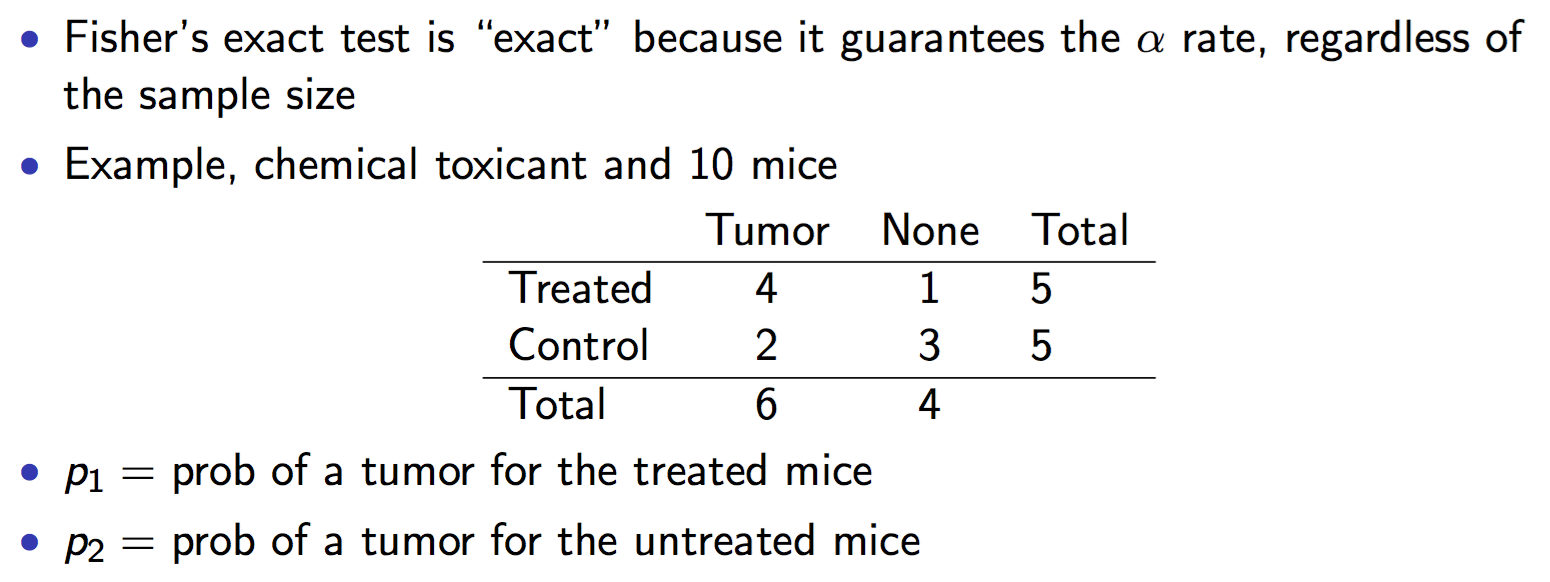
3.1. Use the conditional distribution = hypergeometric, Calculate an exact P-value

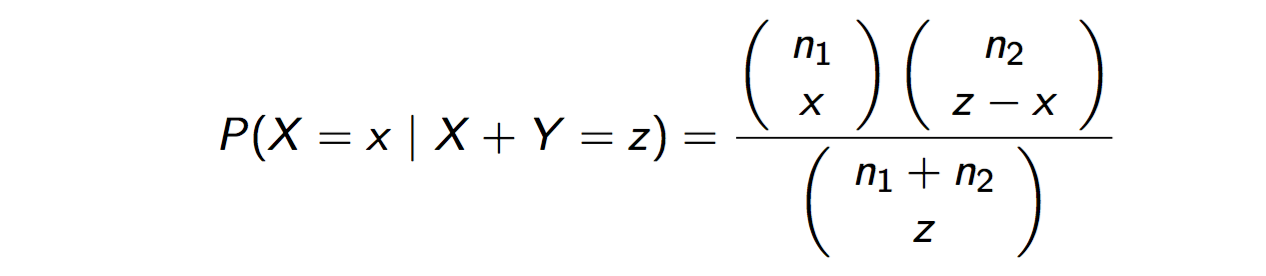
Notes

3.2. R code

fisher.test(matrix(c(17, 25-17, 8, 20-8), ncol=2))
    Fisher's Exact Test for Count Data
# data:  matrix(c(17, 25 - 17, 8, 20 - 8), ncol = 2)
# p-value = 0.07671
# alternative hypothesis: true odds ratio is not equal to 1
# 95 percent confidence interval:
#   0.7990888 13.0020065
# sample estimates:
# odds ratio 
#   3.101466 

4. Chi-squared testing

4.1. An example

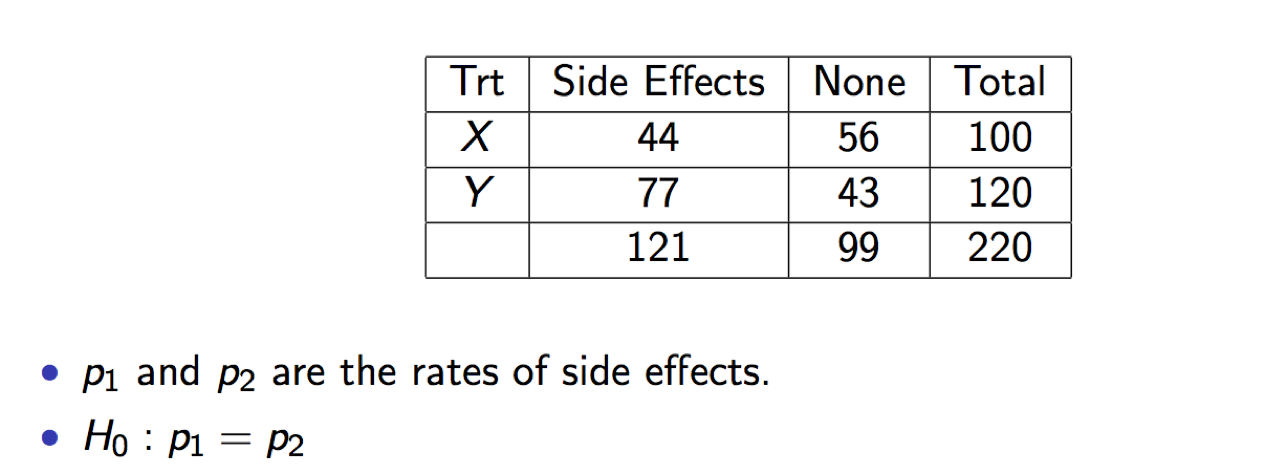
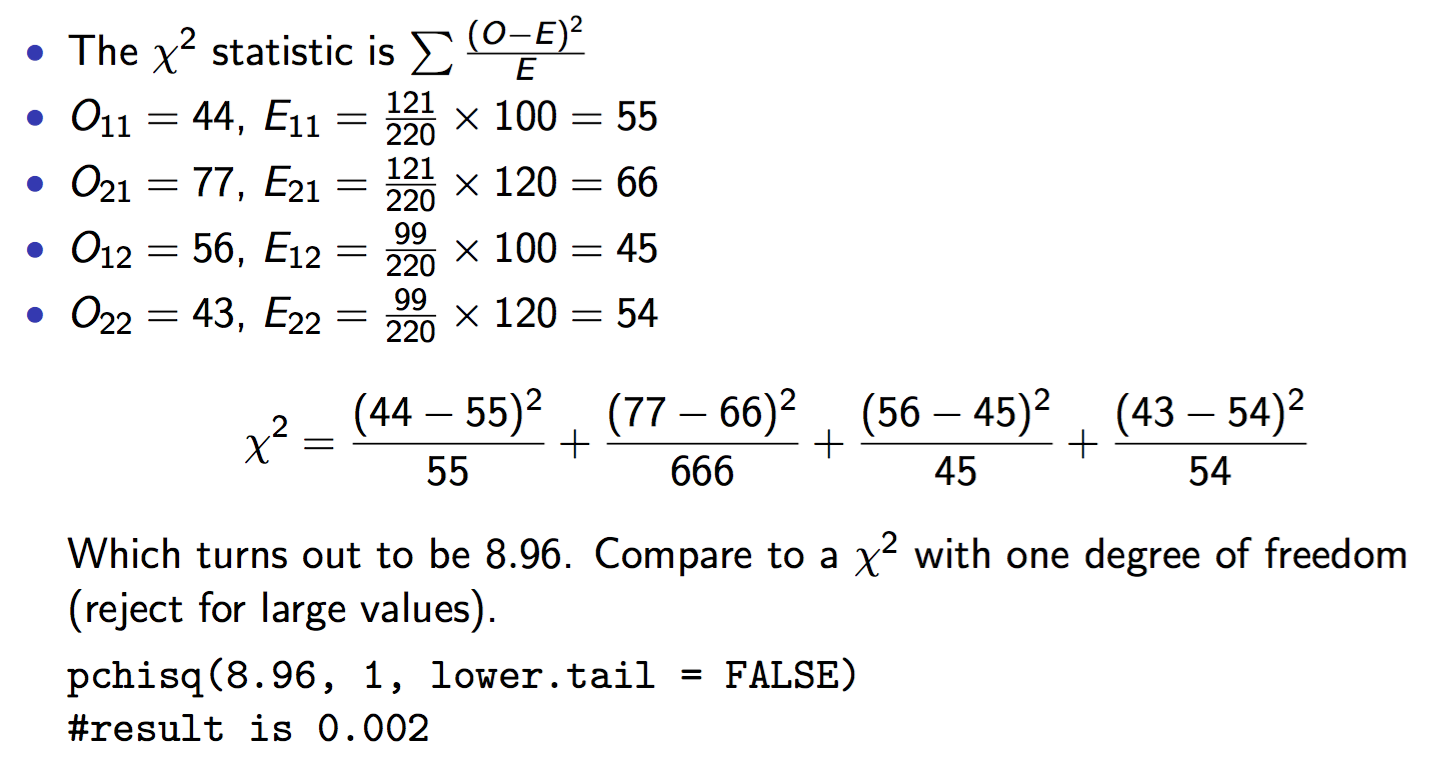
4.2. Notes

4.3. R code

prop.test(c(17,8),c(25,20),correct=FALSE)
# 
#     2-sample test for equality of proportions without continuity correction
# 
# data:  c(17, 8) out of c(25, 20)
# X-squared = 3.528, df = 1, p-value = 0.06034
# alternative hypothesis: two.sided
# 95 percent confidence interval:
#  -0.002016956  0.562016956
# sample estimates:
# prop 1 prop 2 
#   0.68   0.40 

In the case of small samples (low value of n), you must specify correct = TRUE, so as to change the computation of chi-square based on the continuity of Yates